Персональная страничка
Диканева Тараса
Викторовича
Главная \ Преподавательское \ Программирование для начинающих
Введение
Выбор среды программирования
1. Линейные программы: арифметические операторы, стандартные функции и ввод/вывод в текстовом режиме
2. Логические выражения и условный оператор
3. Цикл с параметром (for)
4. Вычисления с помощью рекуррентных соотношений
5. Вложенные циклы
6. Задачи на перебор вариантов
7. Переменные-флаги
8. Переменная - счетчик событий
9. Циклы while и repeat
10. Массивы
11. Процедуры и функции
12. Двумерные массивы
13. Графика в Паскале
14. Символы, строки, текстовые файлы
15. Записи
16. Указатели

11. Процедуры и функции

Предыдущий раздел:

11.10. Процедурные типы

Следующий раздел:

11.12. Правильное составление заголовков процедур и функций

11.11. Пример: Интегрирование методом трапеций

Рассмотрим пример задачи, где могут быть полезны процедурные типы. Пусть требуется создать функцию, производящую численное интегрирование любой функции одной переменной, то есть найти значение

\displaystyle I=\int_{a}^{b} f(x) dx.

Воспользуемся так называемым методом трапеций. Для этого интервал [a, b] разобьем на N равных отрезков. Ширина каждого составит

h=\frac{\displaystyle b-a}{\displaystyle N}.

Концы отрезков будут иметь координаты

x_i=a+i\cdot h, i=0..N.

Оценим интеграл как сумму площадей трапеций, построенных на основе этих отрезков (см. рисунок).

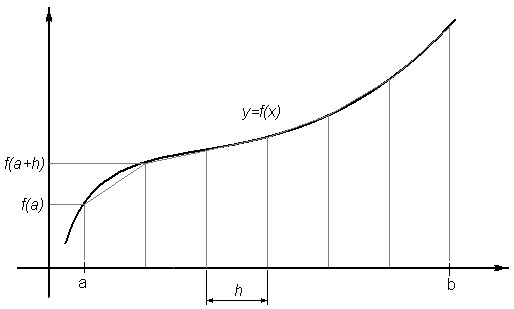
Рис. 1. Вычисление определенного интеграла методом трапеций.

Площадь i-й по счету трапеции составит:

S_i=\frac{\displaystyle f(x_i)+f(x_{i+1})}{\displaystyle 2}\cdot h.

Оценка интеграла, таким образом, дается формулой:

\tilde{I}=\displaystyle \sum_{i=0}^{N-1}S_i=\left(\frac{\displaystyle f(a)+f(b)}{\displaystyle 2}+\displaystyle \sum_{i=1}^{N-1}f(x_i)\right)\cdot h

Очевидно, чем меньше величина h (чем на большее число отрезков разбивается интервал интегрирования), тем более точной получится оценка интеграла.

Составим каркас универсальной функции, вычисляющей такой интеграл:

  type
    TFunc = function (x: real): real;

  function Example (x: real): real;
  {Та функция, от которой в последствии будем брать интеграл}
  begin
    Example:=sin(x);
  end;

  function Integral(a, b: real; f: TFunc): real;
  {<Реализация метода трапеций с использованием функции f>}

  {Начало основной программы}
  begin
    Int:=Integral(0, Pi, Example); {Вызов функции Integral, где в
      качестве параметра передана функция Example, вычисляющая
      синус}
  end.

Вместо Example могла бы стоять произвольная, описанная в программе функция.

Непосредственную реализацию метода трапеций выполните самостоятельно.

Следующий раздел:

11.12. Правильное составление заголовков процедур и функций

Предыдущий раздел:

11.10. Процедурные типы

Добавить комментарий

4 комментария

  1. Alex_Kot 02.09.2015 в 22:19

    В последней формуле предел изменения суммы функций: N-1;
    N-2 неверно.

  2. Taras 03.09.2015 в 00:38

    Снова вы правы. Спасибо, исправил.

  3. Alex_Kot 03.09.2015 в 21:55

    Концептуально в основном понятно. Каша в голове от передачи параметров тоже есть. Программа работает. Все ли верно?
    type
    TFunc = function (x: real): real;
    var
    x, Int: real;
    function Example (x: real): real;
    {Та функция, от которой в последствии будем брать интеграл}
    begin
    Example:=sin(x);
    end;
    function Integral(a, b: real; f: TFunc): real;
    const
    N=1000;
    var
    i: integer;
    h, s: real;
    begin
    h:=(b-a)/N;
    s:=(f(a)+f(b))*h;
    for i:=1 to N-1 do
    begin
    x:=x+h;
    s:=s+f(x);
    end;
    Integral:=s*h;
    end;
    begin
    Int:=Integral(0, Pi, Example); {Вызов функции Integral, где в
    качестве параметра передана функция Example, вычисляющая
    синус}
    Writeln(‘ Int=’, Int);
    end.

  4. Alex_Kot 03.09.2015 в 22:46

    В моем решении ошибка в теле function Integral:
    начальное условие
    s:=(f(a)+f(b))/2;

Добавить комментарий