Персональная страничка
| ||
13. Графика в Паскале
Предыдущий раздел:
Следующий раздел:
13.7. Сдвиг и поворот
Сдвиг на вектор с координатами заключается в добавлении этих координат к координатам каждой точки сдвигаемого объекта:
Часто удобно задавать вектор сдвига его длиной и углом поворота , что как не трудно заметить, означает сдвиг на вектор с координатами:
Поскольку речь идет о сдвиге точки на экране, то для ее прорисовки полученные значения надо округлить до целых. Однако если преобразование сдвига выполняется неоднократно или, за сдвигом следует другие преобразования (например, поворот), то округления, если они делаются после каждого преобразования, будут приводить к накоплению ошибки. Поэтому если координаты преобразуются несколько раз лучше хранить их в вещественных переменных, а округления делать только непосредственно перед рисованием.
Преобразование сдвига, записанное для координат одной точки, можно применять для сдвига любой фигуры. Так, если надо сдвинуть линию, достаточно применить это преобразование к координатам обоих ее концов. Для сдвига окружности, преобразование применяется к координатам ее центра и т.д.

Координаты точек при повороте на угол относительно начала координат преобразуются по закону
Или в матричном виде:
Чтобы осуществить поворот относительно произвольной точки необходимо сделать сдвиг, который перенесет эту точку в начало координат
. После этого надо сделать поворот на требуемый угол и снова сделать сдвиг, который вернет бывшую точку
на место (см. рис.).
|
|
|
Рис. 2. Поворот относительно произвольной точки состоит из сдвига, перемещающего эту точку в начало координат, поворота вокруг начала координат и сдвига, возвращающего центр вращения в исходное место. |
Нетрудно записать такое преобразование одной формулой:
Следующий раздел:
Предыдущий раздел:
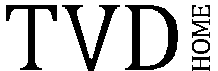

 1. Линейные программы: арифметические операторы, стандартные функции и ввод/вывод в текстовом режиме
1. Линейные программы: арифметические операторы, стандартные функции и ввод/вывод в текстовом режиме
 13.6. Мировые координаты
13.6. Мировые координаты Задание 13: Графика в Паскале
Задание 13: Графика в Паскале
dsb