6. Задачи на перебор вариантов

Предыдущий раздел:

Следующий раздел:

6.1. Перебор вариантов: теория

Имеется целый класс задач, решение которых сводится к перебору различных вариантов, среди которых выбирается такой, который удовлетворяет условию задачи.

Пример 1: Поиск делителей целого числа N.

Целое число K является делителем N, если остаток от деления N на K равен 0. Чтобы найти все делители достаточно перебрать все числа от 1 до N и проверить, являются ли они делителями. Данный алгоритм можно реализовать с помощью программы:

  readln(n);
  for i:=1 to n do
    if n mod i = 0 then
      write(i, '   ');

На этом простейшем примере ясна общая структура решения задач на перебор вариантов. Для организации перебора используется цикл, каждый шаг выполнения которого соответствует рассмотрению одного из вариантов. Внутри цикла стоит проверка, подходит ли данный вариант под условие задачи.

Решая задачи методом перебора, всегда следует подумать, а нельзя ли каким-то образом сократить количество перебираемых вариантов. В данном случае заметим, что любое число делится само на себя и на 1. Поэтому эти варианты можно исключить из перебора. Более того, наибольшим делителем, отличным от самого числа N может быть только N/2, а все числа, большие N/2 заведомо делителями не являются. Учет этих особенностей приводит к более эффективной программе:

  readln(n);
  write(1, '   ');
  for i:=2 to n div 2 do
    if n mod i = 0 then
      write(i, '   ');
  write(n);

Продолжая размышления о сокращении перебора (спасибо комментарию Владимира), заметим, что если i является делителем, то частное от деления на i — тоже делитель. Таким образом, выводя делители парами, можно ограничится перебором до корня из n:

  readln(n);
  writeln(1, '  ', n);
  m:=trunc(sqrt(n));
  for i:=2 to m do
    if n mod i = 0 then
      writeln(i, '  ', n div i);

Конец примера 1.

В приведенном примере вариантом решения являлась переменная i, используемая как счетчик цикла. Не трудно представить себе, задачу, где такое невозможно. Например, вариант может не быть целым числом. В этом случае переменная счетчик цикла выступает как номер варианта, а в цикле требуется совершить еще одно действие: по номеру определить этот самый вариант. То есть вместо схемы:

Перебираем варианты и проверяем, удовлетворяют ли они условию

будем иметь схему

Перебираем номера вариантов, по номеру вычисляем вариант решения, проверяем

Пример 2. Найти минимумы функции с точностью до 0.001 на отрезке от –5 до 5.

Для поиска минимума будем перебирать все числа от –5 до 5 с шагом 0.001. Условием нахождения минимума будем считать то, что значение функции меньше, чем в соседних точках. А именно: . Данный алгоритм можно реализовать с помощью программы:

  Step:=0.001;
  MinX:=-5;
  MaxX:=5;
  VarNumber:=trunc((MaxX – MinX)/Step)+1; {Вычисляем количество
    перебираемых вариантов решения}
  for i:=1 to VarNumber do
  begin
    x:=MinX + (i-1)*step; {Вычисляем вариант, соответствующий номеру i}
    if (sqr(sqr(x))–sqr(x) < sqr(sqr(x-step))–sqr(x-step)) and 
       (sqr(sqr(x))–sqr(x) < sqr(sqr(x+step)) then
     writeln(x);
  end;

Кроме перебора вариантов здесь в начале программы использован еще один важный прием, называемый параметризацией. Такие характеристики как точность и диапазон поиска были записаны в отдельные переменные, а затем вместо чисел использовались имена этих переменных. Такой подход позволяет легче модифицировать программу, если параметры задачи изменятся, программа становится более универсальной. Кроме того, программа становится более понятной, особенно если имена переменных выбраны так, чтобы соответствовать смыслу, хранимого в них параметра (MinX – минимальное значение переменной x и т.п.)

Каждый следующий проверяемый вариант можно также вычислять не по номеру

  x:=MinX + (i-1)*step;

а по предыдущему значению

  x:=x + step;

Очевидно, это ничем не хуже.

Пример 3. Пусть двумя числами (H и V) задано положение коня на шахматной доске. Найдите координаты всех клеток, куда конь может пойти следующим ходом (других фигур на доске нет).

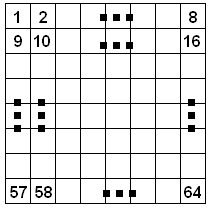
В данном примере, вариантами решения являются координаты клеток, то есть каждый вариант это не одно число, а два. Необходимо придумать способ вычисления варианта (в данном случае номеров горизонтали и вертикали) по его номеру.

Всего клеток 64. Пронумеруем клетки, как показано на рисунке. Теперь, если мы будем перебирать в цикле номера клеток N, необходимо уметь по этим номерам определять номер горизонтали X и вертикали Y. Нетрудно видеть, что номер горизонтали определяется тем сколько раз по 8 клеток надо взять, пока мы не доберемся до числа N:

  X := (N - 1) div 8 + 1;

(N - 1) потому что важно сколько горизонталей заполняют клетки лежащие до N-й, а их как раз N - 1.

Остаток после удаления целого числа раз по 8 клеток позволит вычислить номер вертикали:

  Y := (N - 1) mod 8 + 1;

Теперь, когда мы умеем перебирать варианты, необходимо записать условие того, что данный вариант является решением задачи. Известно, что конь ходит буквой Г, смещаясь на две клетки в одном направлении и на одну в другом. Например, на рисунке показан ход, когда перемещение коня состоит из сдвига на две клетки по вертикали и на одну по горизонтали.

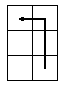
Пусть проверяется клетка с координатами (x, y). Тогда условие сдвига по горизонтали на 2 будет выглядеть так:

  abs(X-H) = 2

Взятие модуля необходимо, чтобы учесть возможность сдвига как вправо, так и влево. Аналогично условие сдвига на одну клетку, например, по вертикали:

  abs(Y-V) = 1

Полное условие возможности пойти на клетку конем будет выглядеть как:

  ((abs(X-H) = 2)and(abs(Y-V) = 1)) or ((abs(Y-V) = 2)and(abs(X-H) = 1))

То есть либо сначала по горизонтали на две клетки, а потом на одну по вертикали либо на две по вертикали, потом на одну по горизонтали.

Теперь, когда ясно как перебирать клетки и как проверять возможность хода, можно написать требуемую программу:

  readln(H, V);	{запрашиваем расположение коня}
  for n:=1 to 64 do
  begin
    X := n div 8 + 1;
    Y := n mod 8;
    if ((abs(X-H) = 2)and(abs(Y-V) = 1)) or ((abs(Y-V) = 2)and(abs(X-H) = 1)) then
      writeln(X, Y);
  end;

В случае, когда как в приведенном примере, каждый вариант задается не одним числом, а несколькими, удобно для перебора использовать вложенные циклы. В данном случае номера вертикали и горизонтали являются целым числами от 1 до 8, поэтому для перебора их значений можно использовать счетчики циклов:

  readln(H, V);
  for X:=1 to 8 do
    for Y:=1 to 8 do
      if ((abs(X-H) = 2)and(abs(Y-V) = 1)) or ((abs(Y-V) = 2)and(abs(X-H) = 1)) then
        writeln(X, Y);

Рассмотрим еще один пример, где вариант задается несколькими числами.

Пример 4. Составить программу-генератор пифагоровых троек. Пифагоровой тройкой называют такие целые числа a, b и c, которые удовлетворяют условию a²+b²=c². Известно, что существует прямоугольный треугольник с такими длинами сторон. Найдем все пифагоровы тройки для c < 5.

Тройное вложение циклов позволит перебрать все возможные комбинации значений трех чисел a, b и c и вывести те из них, которые удовлетворяют заданному равенству.

  MaxC:=25;	{Снова используем параметризацию}
  MaxAB:=trunc(sqrt(MaxC));
  for a:=1 to MaxAB do
    for b:=1 to MaxAB do
      for c:=1 to MaxC do
        if a*a+b*b = c*c then
        begin
          write(a, '   ', b, '   ', c);
          writeln;
        end;

Как всегда при решении задачи методом перебора, следует задуматься, можем ли мы сократить число перебираемых вариантов. Оказывается, можно ограничиться только перебором a и b, а c вычислять по теореме Пифагора . Вычисленное таким образом c может оказаться нецелым, поэтому условие задачи для него проверять все равно необходимо.

  MaxC:=25;	{Используем параметризацию}
  MaxAB:=trunc(sqrt(MaxC));
  for a:=1 to MaxAB do
  begin
    for b:=1 to MaxAB do
    begin
      c:=round(sqrt(a*a+b*b));
      if a*a+b*b = c*c then
      begin
        write(a, '   ', b, '   ', c);
        writeln;
      end;
    end;
  end;

Следующий раздел:

Предыдущий раздел:

Добавить комментарий