|
Персональная страничка
| |
1. Линейные программы: арифметические операторы, стандартные функции и ввод/вывод в текстовом режиме
1. Линейные программы: арифметические операторы, стандартные функции и ввод/вывод в текстовом режиме
Предыдущий раздел:
1.6. Ввод/вывод в текстовом режимеСледующий раздел:
Контрольная работа №11.7. Задачи на составление арифметических выражений
Хотя для наглядности речь в задачах может идти о столбах, шагах или распиливания бревна, полностью аналогичные задачи программистам приходится решать на каждом шагу (при работе с массивами, при вычислении количества шагов в циклах и т.д.) Все выражения, которые вам требуется составить, взяты из реальной программистской практики.
Прорешать данные задачи также полезно в связи с тем, что многие не умеют решать задачи в общем виде, когда вместо конкретных чисел используются буквенные обозначения. Кроме того, большинство выпускников обычных школ плохо представляют себе, что значит думать над задачей. Они могут прилежно заучить правила написания и смысл операторов языка, но когда надо изобрести способ решить задачу с их помощью, не понимают, что же им делать.
В данном случае мы имеем дело с простейшей ситуацией – по сути, требуется придумать программу, состоящую из одной строки. Набор операций дан, требуется их скомбинировать так, чтобы получился требуемый результат. Решение данных задач позволит выработать правильный подход и настрой для работы в ситуации когда «неизвестно что делать».
Задания:
Используя арифметические операторы (+, -, *, /, div, mod), а также функции round(), trunc() и abs(), составьте арифметические выражения для вычисления следующих величин:
1. n-е четное число (первым считается 2, вторым 4 и т.д.)
2. n-е нечетное число (первое равно 1, второе 3 и т.д.)
3. В очереди стоят n людей, сколько человек находится между i-м и k-м в очереди.
4. Сколько нечетных чисел на отрезке (a, b), если a и b – четные? Если a и b – нечетные? a –четное, b – нечетное?
5. Сколько полных минут и часов содержится в x секундах?
6. В доме 9 этажей, на каждом этаже одного подъезда по 4 квартиры. В каком подъезде, и на каком этаже находится n-я квартира.
7. Старинными русскими денежными единицами являются: 1 рубль – 100 копеек, 1 гривна — 10 копеек, 1 алтын — 3 копейки, 1 полушка — 0,25 копейки. Имеется А копеек. Запишите выражения для представления имеющейся суммы в рублях, гривнах, алтынах и полушках.
8. Стрелка прибора вращается с постоянной скоростью, совершая w оборотов в секунду (не обязательно стрелка прибора, может быть это волчок в игре «Что? Где? Когда?» и т.п.) Угол поворота стрелки в нулевой момент времени примем за 0. Каков будет угол поворота через t секунд?
9. Вы стоите на краю дороги и от вас до ближайшего фонарного столба x метров. Расстояние между столбами y метров. На каком расстоянии от вас находится n-й столб?
10. Та же ситуация, что и в предыдущей задаче. Длина вашего шага z метров. Мимо скольких столбов вы пройдете, сделав n шагов.
11. x – вещественное число. Запишите выражение, позволяющее выделить его дробную часть.
12. x – вещественное число. Запишите выражение, которое округлит его до сотых долей (останется только два знака после запятой).
13. n – целое число. Запишите выражение, позволяющее узнать его последнюю цифру.
14. n – четырехзначное целое число. Запишите выражение, позволяющее узнать его первую цифру.
15. Оператор div в Паскале работает только для целых чисел. Составьте выражение, позволяющее получать целую часть от деления вещественных чисел.
16. Выразите операцию mod через другие арифметические операции.
17. x – вещественное число. Запишите выражение, которое даст +1, если x>0 и -1, если x<0 (при x=0 выражение будет неопределено).
18. n и m – целые числа. Запишите выражение, которое давало бы 0, если n кратно m и 1, если не кратно.
19. От бревна длиной L отпиливают куски длиной x. Сколько кусков максимально удастся отпилить.
20. Бревно длиной L распилили в n местах. Какова средняя длина получившихся кусков?
21. Резиновое кольцо диаметром d разрезали в n местах. Какова средняя длина получившихся кусков?
22. На прямой через равные промежутки располагается n точек. Расстояние от первой до последней равно L. Чему равно расстояние от первой точки до i-й? А от k-й до последней? А от i-й до k-й?
23. Известно, что приближенные формулы для вычисления синуса и косинуса работают тем точнее, чем меньше значение аргумента. Поскольку синус и косинус 2π-периодические функции (sin(x) = sin(x+2πn) , где n – любое целое число), то можно вычисление синуса от любого аргумента привести к вычислению синуса от аргумента, лежащего в диапазоне от 0 до 2π. Запишите формулы, позволяющие:
(а) привести положительный угол x в диапазон от 0 до 2π.
(б) аналогично для отрицательного угла.
24. Пусть дано трехзначное число x (например, 123). Составьте выражения, которые позволят вычислить первую, вторую и третью цифру этого числа (числа 1, 2 и 3 в примере). Для облегчения поиска решения имейте в виду, что для двузначного числа первая цифра дается выражением
d1:=x div 10;
а вторая выражением
d2:=x mod 10;
Следующий раздел:
Предыдущий раздел:
327 комментариев
|
Copyright 2010 by Dikanev Taras
|
|
Добрый день. Интересный и нужный Ваш сайт. Попытался порешать задачки Ваши. И ни как не получается «въехать» в некоторые. А есть гда нибудь ответы на них, что бы можно было подглядеть, как решения Ваших задач должно выглядеть? Т.е. наглядное правильное решение. С Уважением, Александр.
Привет! Ответов нет. Но, если что-то совсем не получается, можно обсудить. Мне не очень хочется писать готовый ответ, но зато я могу дать какой-нибудь намек, совет, задать наводящие вопросы и т.п.
День добрый.Решаю задачки.Очень интересные и занимательные.
Споткнулся на №18.Так сяк пробовал не получается.Подкиньте
идейку.Заранее благодарен.
Знаете, совершенно забыл, какое решение я имел в виду, когда сочинял эту задачу (по воспомиинаниям что-то простое). Пришлось придумывать новое и оно действительно заметно сложнее прочих.
В общем моя идея в том чтобы сначала получить дробную часть от деления n на m:
Если числа кратны, то получится желаемый ноль. Иначе число между 0 и 1, которое надо превратить в единицу. Немного обобщив задачу, можно сказать, что требуется дополнить дробное число до ближайшего целого числа. Вообще-то в Паскале есть соответствующая функция — ceil, но в задании о ней ничего не говорится, так что надо сочинить ее аналог.
Это можно сделать, например, так:
y = round(x + 0.5 — 1e-20);
//Вариант 2
y = trunc(x + 1 — 1e-20);
Еще один вариант решения даст 1 если числа кратны и 0, если нет:
x = n/m — trunc(n/m);
//Делаем из нуля единицу
y = 1 — x;
//Если числа не кратны, то y<1, так что остается сделать лишь
z = trunc(y);
Однако, нам надо наоборот 0, если они кратны. Остается придумать выражение, превращающее 0 в 1, а 1 в 0. Это не сложно:
y = 1 — x;
//заменит одно на другое
Еще один способ пришел в голову. Надо из n и m получить выражение, которое отрицательно, если они кратны и положительно, если нет. Например, так:
Дальше можно воспользоваться решением задачи 17 и получить из этого числа -1, если кратны, и +1, если нет. А уже из этих чисел можно получить 0 и 1:
//Чтобы получить 0 или 1 делаем
y = (x + 1)/2;
Здравствуйте! Я в этом деле совсем новичок, поэтому можно Вас попросить помочь и проверить меня??)
Проверить можно. Пришлите свои решения на tvdikanev@yandex.ru, я посмотрю.
Доброй ночи.Все задачи решил достаточно быстро, а №18 никак не могу решить.Мне кажется, что у этой задачи нет решения, или нужны дополнительные условия, например, n меньше m.Возможно, я ошибаюсь, тогда хотел бы узнать решение.Заранее благодарен.
P.S. Чтобы не отвлекать других решающих можно отправить на info.papirus@yahoo.com
program hggh; uses crt; var n,m,g: integer; BEGIN writeln('введите n'); readln(n); writeln('введите m'); readln(m); g:=((n mod m) + m-1) div m; writeln('ответ', g); END.Действительно. Хороший вариант.
срочно № 4!
скиньте ответы сюда на эти вопросы и на контрольные тоже, а то так не пронятно( mba1994@inbox.ru
Просто ответы смотреть не хорошо. Если совсем непонятно, о чем речь, можно обсудить первые несколько задач, а так надо самому решать.
как делать 11 и 12 ??
вроде так получается:
11. …
12. …
Taras, проверьте пожалуйста.
Правильно.
Ответы стер, чтобы не портить другим людям удовольствие.
привет, пожалуйста объясните что требуется сделать в 1 и 2 задаче?
Ну, например, в первой задаче нужно придумать формулу, куда бы вместо n можно было подставить
любой номер и получить соответствующее четное число. Правильный ответ к задаче: 2*n
Хотим узнать 2-е четное число, подставляем n = 2:
2*n = 2*2 = 4.
Хотим узнать 135-е, подставляем n = 135:
2*n = 2*135 = 270.
Это еще называется решить задачу в обшем виде.
спасибо, n*2-1 ко второму правильно?
Правильно ))
5 задание. могу сделать что бы показывало сколько минут в х секундах и часов в них же, не могу сделать сброс оставшихся минут с часа на показатель минут. как????
Я не совсем понял в чем проблема. Напиши подробнее, что ты делаешь и что не получается.
вообщем справился с 5 задачей так:
program Proga;
var
x,y: integer;
begin
write(‘секунды ‘);
readln(x);
y:=x div 60;
writeln(y div 60,’ часов. ‘,y mod 60,’ минут(ы).’);
end.
но не понял как работает оператор mod
Ну, так mod — остаток от деления двух целых чисел.
Делишь, например, 125 на 60. 60 целиком укладывается в 125-ти два раза (2 — целая часть от деления, то есть div), а что поле этого осталось — это mod.
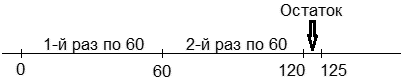
Т.е в данном примере значение mod = 5?
Да
пожалуйста напишите задачу № 9…никак не пойму))) заранее спасибо!!!
Давать ответы — это не правильно. А в качестве совета: попробуйте порешать задачу для конкретных x, y и n. До ближайшего столба 5 метров, между столбами 20, сколько от вас до 3-го, 4-го, 5-го? А что, если между столбами на 20, а 15 метров?
Общая формула для решения этой задачи: х+у(n-1), где n- число фонарей. Но как составить программу???
не понимаю…напишите программу, пожалуйста!!! очень нужно!)))
Вообще-то, целью является именно составление формулы. Программу писать не надо. Если очень хочется, то все написание сводится к вводу исходных данных, вычислению по формуле и выводу результата. Как-то так:
var x, y, s: real; n: integer; begin readln(x, y, n); s := x + y * (n-1); writeln('s = ', s); end.Оказывается вот как!!! спасибо Вам большое)))
Помогите пожалуйста с 11 задачей, никак не могу понять как формулу составить чтобы дробную часть выделял :/
Подумайте, может быть, знание целой части (функция trunc) вам поможет.
Здравствуйте! Подскажите пож. №6 так будет или есть способ проще?
program ddd;
var
a,c,x,y,z: integer;
b,d: real;
begin
write(‘номер квартиры ‘); readln(a);
b:=a div 36+1; d:=a mod 36/4+1;
writeln(trunc(b),’ подъезд ‘,trunc(d),’ этаж ‘);
end.
забыл убрать ненужные переменные…
Не совсем так, поскольку у вас 36-я квартира окажется во втором подъезде, а 4-я квартира на 2-м этаже.
Кстати, от trunc’ов можно избавиться. trunc(b) вообще не нужен (div и так дает целое число), а trunc(d) это целая часть от деления «/», что опять таки можно заменить на div.
возможно так?
но я не могу понять как исправить, у меня получается 1кв на 0 этаже. подскажите пожалуйста формулу, по готовой формуле пойму быстрее чем пол дня голову ломать ;=)
program ddd;
var
a,b,c,d: integer;
begin
write(‘номер квартиры ‘); readln(a);
b:=a div 36; d:=36*b; c:=(a-d)div 4;
writeln(b+1,’ подъезд ‘,c,’ этаж ‘);
end.
прошу прощения, предложенное выще решение неверно…
Знаете, я уверен, что польза от ломанья головы гораздо больше, чем от знания или даже понимания решения.
задача 11
подскажите пожалуйста это решение верно?
program qwerty;
var
x: real;
begin
write(‘введите число с дорбной частью ‘); readln(x);
writeln(x-trunc(x));
end.
если да, то почему при значении х= 9.37 мы получаем 0.369999999999999 ?, или при любом значении х>7 с дробъю .36, .37, .38, .39
Ну это же почти 0.37 :)
Дело в том, что 0.37 в двоичной системе счисления это бесконечная периодическая дробь:
0.01(01111010111000010100)
Но компьютер работает только с конечным числом нулей и единиц (конкретно у типа real в мантиссе 52 бита). То есть реально в памяти хранится не 0.37, а другое число — результат обрезания бесконечной дроби до 52 значащих цифр. Как именно происходит «обрезание» и как ведут себя такие приближенные числа при вычислениях определяется стандартом IEEE 754.
Согласно этому стандарту число с плавающей точкой имеет вид
где s знак (0 ~ «+», 1 ~ «-«), m — мантисса, p — порядок. В памяти лежит так:
Мантисса представляет из себя дробь, начинающуюся с 0.1… То есть 0.37 будет иметь мантиссу
0.10111101011100001010001111010111000010100011110101110
и порядок -1.
Теперь рассмотрим, что же произойдет, если мы проделаем операцию (x + 0.37) — x. Пусть x = 9. В двоичной системе это 1001. Прибавив это число получим мантиссу
0.10010101111010111000010100011110101110000101000111101
01110и порядок 4. Зачеркнутые цифры в конце будут отброшены. Вычитая из этого числа 9 получим мантиссу
0.10111101011100001010001111010111000010100011110100000
то есть число меньше того, что было в начале. Величина погрешности зависит от количества цифр в двоичном представлении x. 7 ~ 111 (3 цифры), 8 ~ 1000 (4 цифры). writeln выводит 15 десятичных цифр, то есть чтобы заметить эффект нужна погрешность больше 0.5 * 10-15. При семерке погрешность еще не достаточна. А начиная с восьмерки — в самый раз.
Это пример влияния так называемых ошибок округления при операциях с плавающей точкой. Особенно интересно становится тогда, когда в процессе сложных вычислений возникшие таким путем ошибки начинают накапливаться. Солдаты гибнут, ракеты падают и, вообще, это один из сценариев конца света. Сложность вычислений в управляющих нашей жизнью компьютерах будет расти. Со временем станет невозможно предусмотреть и отследить распространение ошибок округления, что приведет к глобальной техногенной катастрофе.
Добрый день. Подскажите пожалуйста правильно ли я решил задачу № 6
program asd;
var
x: integer;
begin
write(‘номер квартиры ‘);
readln(x);
writeln(‘подъезд ‘, …);
writeln(‘этаж ‘, ( trunc ( trunc (x-0.01)) mod …);
end.
Правильно ))
Ответы стер, чтобы не мешать другим людям самим догадаться.
trunc’и лишние. Первый не нужен — он берется от и так уже целого числа. Что касается trunc(x-0.01) при целом значении x, то подумайте, как можно то же самое сделать проще.
program zd4;
var a,b,c,d:integer;
m:real;
begin
writeln(‘Введите число a’) ;
readln(a);
writeln(‘Введите число b’);
readln(b);
if (a mod 2=0) and (b mod 2=0) then
m:=(((b-a-2)/2)+1)
else if (a mod 2 <> 0) and (b mod 2 <> 0) then
m:=(((b-a)/2)-1)
else
if (a mod 2=0) and (b mod 2 <> 0) then
m:=((b-a-1)/2);
writeln(m);
end.
Вот смотрю, всё решается тут простыми в общем то способами, а вот увы эта задача у меня решалась только так, может кто скажет, как можно её решить более простым способом?) Потому что решал я её не по теме этой, а просто как знал
задача номер 4
В принципе, так и предполагалось, что для каждого случая будет свой вариант формулы. Так что решение нормальное. Разве что 1-е выражение упростится, если раскроешь скобки.
Но, если хочешь без if’ов, то можно и без них:
m := (b-a)/2 — (a mod 2 + b mod 2)/2;
не могу понять восьмую задачу. Сколько на сколько градусов в секунду стрелка поворачивается
program zd10;
var a,n,b,c,d,w,t:real;
begin
writeln(‘введите частоту вращения w’);
readln(w);
writeln(‘время вращения t’);
readln(t);
n:=w*t;
a:=round(360*((w*t)-(round(w*t))));
writeln(a);
end.
Можно ли решить проще ? Кажется, что не рациональным способом всё решал, но увы по другому никак не мог получить значение угла стрелки не превышающие 360, а то всё время путь быть в градусах.
a:=round(360*((w*t)-(trunc(w*t)))); изменил, а то некоторые не подходят
Внешний round надо убрать — в дробном числе градусов ничего плохого нет. А в остальном правильно. Проще, думаю, не получится.